A Sallen-Key 3-Pole Butterworth Active Highpass Filter: Design Sheet(DS2)

A Sallen-Key 3-Pole Butterworth Active Highpass Filter - Design Sheet (DS2)

by John-Paul Bedinger

Of the various topologies you can select for making active filters, the Sallen-Key uses the least number of filter components. Furthermore, a 3-pole response (18 db/oct) is possible using only 1 op-amp. Below is a brief mathematical description on how to compute the component values for a Butterworth (steepest response with no ripple) 3-pole highpass filter with selectable output gain.

Diagram 1: A 3-pole Sallen-Key highpass filter with output gain.

Looking at node 3b (where v3 = v3a = v3b) , the node voltage equation can be re-written to be:

where and M defines the AC gain of the circuit in the passband (Eq. 1 and 2).

The rest of the node voltage equations can be written:

(Eq. 3)

(Eq. 4)

(Eq. 5)

When solved for the filter transfer function H(s) = Vout/Vin, we get:

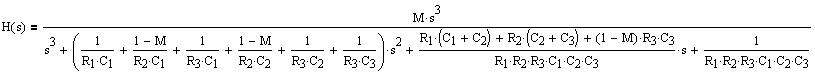
(Eq. 6)

Note that the standard form of a 3-pole Butterworth highpass filter at cutoff frequency 1 rad/sec is:

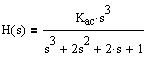(Eq.7) where Kac is the AC gain of the filter, the same as our M.

Equating like terms in Equations 7 and 6 gives the solve block:

(Eq.8)

(Eq.9)

(Eq.10)

(Eq.11)

We choose our output gain: Kac = M = 4 (12 dB)

Also, we choose values for components: C1= 100 uF, C2= 100uF, C3= 100uF, R5= 10 k-ohms

Solving now for R1, R2, R3,and R4 gives (exact):

R1= 5 k-ohms, R2= 20 k-ohms, R3= 10 k-ohms, R4= 30 k-ohms

Rounding R1-R4 to standard EIA 1% tolerance decade values gives:

R1= 4.99 k-ohms, R2= 20 k-ohms, R3= 10 k-ohms, R4= 30 k-ohms

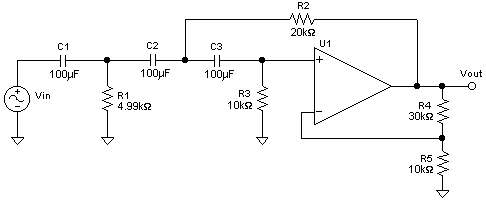
Diagram 2: A 3-pole Sallen-Key Butterworth highpass filter with cutoff at 1 rad/sec and a gain of 4 (12dB).

Practical Notes:

For different gain values you can refer to my table below, or resolve the solve block with a different value of Kac. Use solutions only with all real positive roots. If you have Mathcad(TM), you can download this zipped Mathcad worksheet to help you.
C1, C2, and C3 from the table can be scaled together by a factor y, which should be done so that the source impedance Rin is much less than the magnitude of the impedance (Rin + C1) at the cutoff frequency Fc. This will set the cutoff frequency to 1/y rad/sec.
R1, R2, and R3 from the table can be scaled together by a factor x, which will set the cutoff to 1/(x *y) rad/sec, or:

Fc = 1/(2*3.1416*x*y) Hz (Eq. 12)

M	0dB	6dB	12dB	18dB	24dB	30dB	36dB
R1(ohms)	7180.57	5862.23	5000	4223	3531.2	2933.18	2425.61
R2(ohms)	2819.43	11533.14	20000	31821.84	49433.83	76312.84	117808
R3(ohms)	49394.66	14790.74	10000	7441.38	5728.67	4467.49	3499.48
R4(ohms)	0	10000	30000	70000	15000	31000	63000
R5(ohms)	infinite	10000	10000	10000	1000	1000	1000
C1(Farads)	100.E-6	100.E-6	100.E-6	100.E-6	100.E-6	100.E-6	100.E-6
C2(Farads)	100.E-6	100.E-6	100.E-6	100.E-6	100.E-6	100.E-6	100.E-6
C3(Farads)	100.E-6	100.E-6	100.E-6	100.E-6	100.E-6	100.E-6	100.E-6

M	42dB	48dB	54dB	60dB	66dB	72dB	78dB
R1(ohms)	1998.55	1640.85	1342.31	1094.1	888.6151	719.3089	580.4752
R2(ohms)	182295.4	282964.2	440633.6	688213.9	1077780	1691800	2660920
R3(ohms)	2744.79	2153.77	1690.71	1328.07	1044.13	821.7427	647.4178
R4(ohms)	127000	25500	51100	102300	20470	40950	81910
R5(ohms)	1000	100	100	100	10	10	10
C1(Farads)	100.E-6	100.E-6	100.E-6	100.E-6	100.E-6	100.E-6	100.E-6
C2(Farads)	100.E-6	100.E-6	100.E-6	100.E-6	100.E-6	100.E-6	100.E-6
C3(Farads)	100.E-6	100.E-6	100.E-6	100.E-6	100.E-6	100.E-6	100.E-6

Table 1: Prototype component values for a Butterworth highpass filter response at 1 rad/sec.

Example:

We want Fc= 80 Hz, C1= 0.1uF, C2= 0.1uF, and C3= 0.1uF, and a gain of 30 dB. The source resistance is 220 ohms or less.

Use Table 1 for 30dB prototype values, then scale y for the correct capacitor range:

The scale factor y is 0.1uF/100uF, or y = 0.001. Thus, 80 Hz = 1/(2*3.1416*x*0.001). Solving for x gives: x = 1.989

Scaling R1, R2, R3,and R4 by x gives:

R1= 5834.1 ohms, R2= 151786 ohms, R3= 8885.8 ohms, R4= 31 k-ohms, R5=1 k-ohm

Rounding R1-R4 to standard EIA 1% tolerance decade values gives:

R1= 5.9 k-ohms, R2= 150 k-ohms, R3= 8.87 k-ohms, R4= 30.9 k-ohms, R5=1 k-ohm

The magnitude of (C1 + Rin) at 80Hz is:

(1/(2*3.14*80*0.1e-6)^2+220^2)^.5 = 19.9 k-ohm at 80 Hz.

Since the combined impedance of 19.9 k-ohm at the cutoff frequency is much greater than the 220 ohm source resistance by itself, the value for C1 should work well.

Change Log:

v.1.0.1 Made MathCad file a zip file.

v.1.0 Initial release.

Questions or feedback? E-mail me at jpbedinger@hotmail.com

Do not duplicate, distribute, or modify without my expressed written permission.

Disclaimer: The author is not responsible for any damages resulting from the content or application of this document. Use at your own risk.