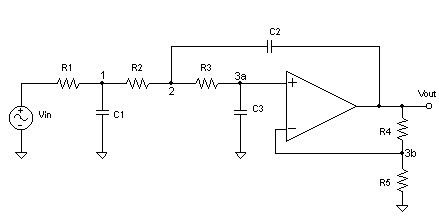
A Sallen-Key 3-Pole Butterworth Active Lowpass Filter: Design Sheet (DS1)

A Sallen-Key 3-Pole Butterworth Active Lowpass Filter - Design Sheet (DS1)

by John-Paul Bedinger

Of the various topologies you can select for making active filters, the Sallen-Key uses the least number of filter components. Furthermore, a 3-pole response (18 db/oct) is possible using only 1 op-amp. Below is a brief mathematical description on how to compute the component values for a Butterworth (steepest response with no ripple) 3-pole lowpass filter with selectable output gain.

Diagram 1: A 3-pole Sallen-Key lowpass filter with output gain.

Circuit Analysis:

Looking at node 3b (where v3 = v3a = v3b) , the node voltage equation can be re-written to be:

(Eq. 1)

Let: Then: (Eq. 2)

The rest of the node voltages can be written:

When solved for the filter transfer function H(s) = Vout/Vin, we get: H(s)=

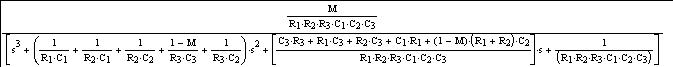(Eq. 3)

Note that the general form of a 3-pole Butterworth lowpass filter at cutoff frequency 1 rad/sec is:

H(s) = (Eq. 4)

Equating like terms in Equations 3 and 4 gives the solve block:

where Kac = M.

We choose our output gain: Kac = 3 (9.5 dB)

Also, we choose values for components: C1= 3000 uF, C2= 1000uF, C3= 1000uF, R5= 10 k-ohms

Solving now for R1, R2, R3,and R4 gives:

R1= 816.46 ohms, R2= 481.26 ohms, R3= 848.33 ohms, R4= 10 kohms

Rounding R1-R4 to standard EIA 1% tolerance decade values gives:

R1= 825 ohms, R2= 487 ohms, R3= 845 ohms, R4= 20 k-ohms

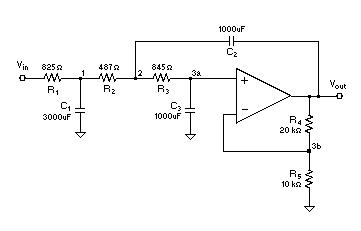
Diagram 2: A 3-pole Sallen-Key Butterworth lowpass filter with cutoff at 1 rad/sec and a gain of 3.

Practical Notes:

For different gain values you can refer to my table below, or resolve the solve block with a different value of Kac. Use solutions only with all real positive roots. If you have Mathcad(TM), you can download this zipped Mathcad worksheet to help you.
R1, R2, and R3 from the table can be scaled together by a factor x, which should be done so that R1 is much greater than the source impedance at Vin. This will set the cutoff to 1/x rad/sec.
C1, C2, and C3 from the table can be scaled together by a factor y, which will set the cutoff frequency to 1/(x*y) rad/sec, or:

Fc = 1/(2*3.1416*x*y) Hz

M(Kac)	0dB	6dB	12dB	18dB	24dB	30dB	36dB
R1(ohms)	1292	15652	1624	4305	3246	1437	3234
R2(ohms)	2093	14694	4067	1750	2134	16260	7198
R3(ohms)	3698	4348	15144	13276	1444	42794	42950
R4(ohms)	0	10000	30000	70000	15000	31000	63000
R5(ohms)	infinite	10000	10000	10000	1000	1000	1000
C1(farads)	1.E-3	100.E-6	1.E-3	1.E-3	1.E-3	1.E-3	1.E-3
C2(farads)	1.E-3	100.E-6	100.E-6	100.E-6	100.E-6	10.E-6	10.E-6
C3(farads)	100.E-6	100.E-6	100.E-6	100.E-6	1.E-3	100.E-6	100.E-6

M(Kac)	42dB	48dB	54dB	60dB	66dB	72dB	78dB
R1(ohms)	1640	1242	2243	1030	1137	1700	6053
R2(ohms)	13615	69066	32123	185004	285242	136533	47723
R3(ohms)	4479	116556	138815	5249	308473	430832	346170
R4(ohms)	127000	25500	51100	102300	20470	40950	81910
R5(ohms)	1000	100	100	100	10	10	10
C1(farads)	1.E-3	1.E-3	1.E-3	1.E-3	1.E-3	1.E-3	1.E-3
C2(farads)	10.E-6	1.E-6	1.E-6	1.E-6	100.E-9	100.E-9	100.E-9
C3(farads)	1.E-3	100.E-6	100.E-6	1.E-3	100.E-6	100.E-6	100.E-6

Table 1: Prototype component values for a Butterworth filter response at 1 rad/sec.

Example:

We want Fc= 1000 Hz, C1= 0.1uF, C2= 0.1uF, and C3= 0.1uF, and a gain of 6 dB. The source resistance is 10 ohms.

Use Table 1 for 6dB prototype values, then scale y for the correct capacitor range:

The scale factor y is 0.1uF/100uF, or y = 0.001. Thus, 1000 Hz = 1/(2*3.1416*x*0.001). Solving for x gives: x = 0.159

Scaling R1, R2, R3,and R4 by x gives:

R1= 2.489 kohms, R2= 2.336 kohms, R3= 691.3 ohms, R4= 10 kohms, R5=10 kohms

Rounding R1-R4 to standard EIA 5% tolerance decade values gives:

R1= 2.4 kohms, R2= 2.4 kohms, R3= 680 ohms, R4= 10 kohms, R5=10 kohms

Since 2.4 kohms >> 10 ohms source resistance, the value for R1 should work well.

Change Log:

v.1.3.1 Made MathCad file a zip file.

v.1.3 Changed 66db gain resistors in Table 1. (Older values were ok as well)

Moved design sheet to new location on server.

Changed title and included design sheet identifier (DS1)

v1.2 Made R5=10k in solve block constants to match pictured results.

Corrected component values for gains above 36dB in Table 1.

Made bigger JPEG for diagram 1.

Added link to Mathcad(TM) worksheet file.

Made various small text formatting changes, and switched to Arial font.

Added this change log.

Questions or feedback? E-mail me at jpbedinger@hotmail.com

Do not duplicate, distribute, or modify without my expressed written permission.

Disclaimer: The author is not responsible for any damages resulting from the content or application of this document. Use at your own risk.